阅读数模培训PPT的笔记

非线性规划模型

例题1 供应与选址

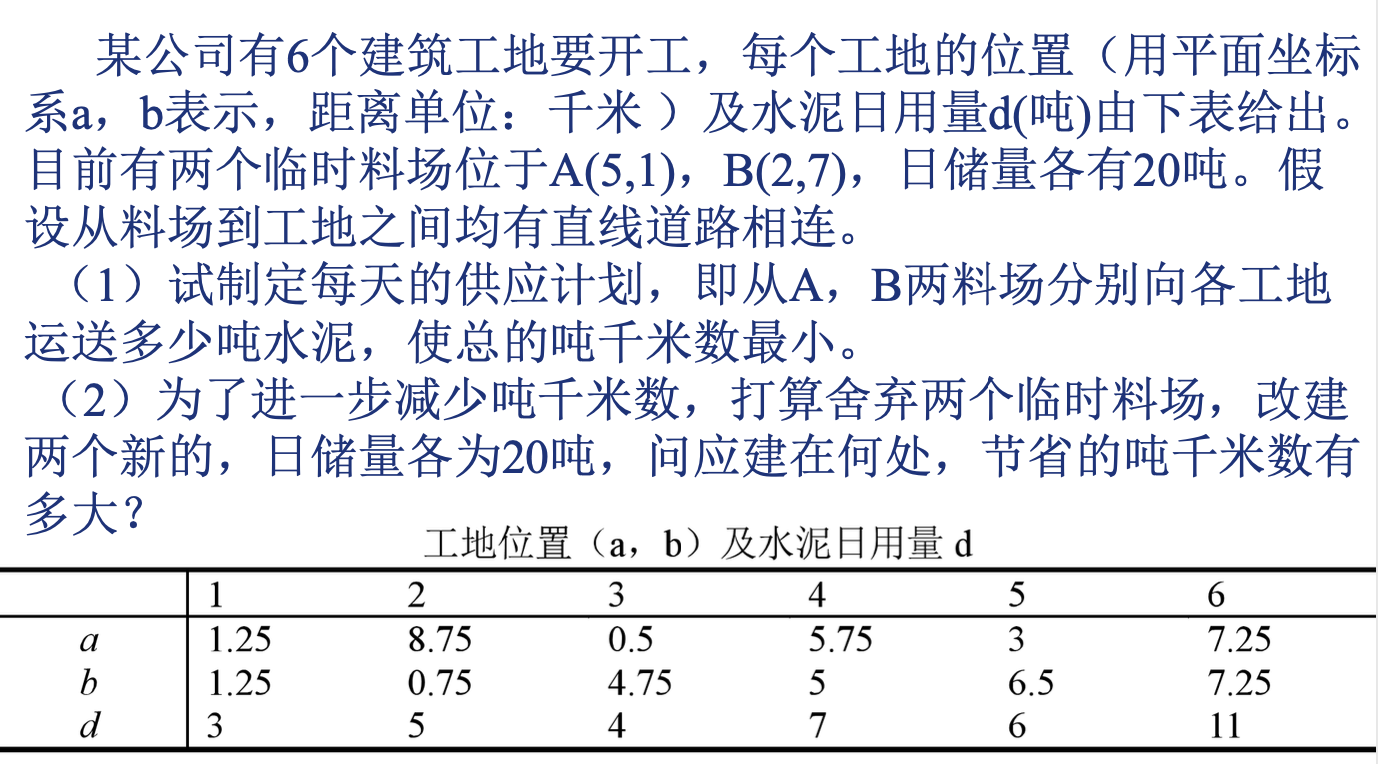
一、基本假设

从料场到使用建筑工地之间均有支线道路相连。

二、符号规定

$(a_i,b_i)$表示第i个建筑工地的坐标；
$d_j$表示第i个建筑工地的需求量；
$(x_j,y_j)$表示第j个料场的坐标；
$e_j$表示第j个料场到储备量；
$x_{ij}$表示第j个料场到第i个建筑工地的运输量；
三、模型分析

四、模型的求解
使用原料场——线性规划问题
新建料场——非线性规划问题

MATLAB求解——fmincon函数

fmincon函数格式

fmincon函数用于求解非线性规划问题，其调用格式为：

1	[x, fval, exitflag, output] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options)

参数说明：

fun: 目标函数(需要自定义函数内容)
x0: 变量的初始值
A, b: 不等式约束条件的系数矩阵和右侧常数向量
Aeq, beq: 等式约束条件的系数矩阵和右侧常数向量
lb, ub: 变量的下界和上界
nonlcon: 非线性约束条件(也是一个自定义函数)
options: 优化选项

nonlcon函数用法

function [c, ceq] = nonlcon(x)
c = [x(1)^2 + x(2)^2 - 1;x(1)-2];
%表示不等式约束条件集合，当c中每一项都<=0时，表示约束条件成立
ceq = [];%表示等式约束条件

五、MATLAB程序

%函数文件liaoch.m
function [f,g]=liaoch(x)
a=[1.25 8.75 0.5 5.75 3 7.25 ];
b=[1.25 0.75 4.75 5 6.5 7.75 ]; d=[3 5 4 7 6 11];
e=[20 20];
f1=0;
for j=1:6
s(j)=sqrt((x(13)-a(j))^2+(x(14)-b(j))^2);
f1= f1 + s(j)*x(j); % A(x13,x14)到各工地的吨公里数 
end
f2=0;
for i=7:12
s(i)=sqrt((x(15)-a(i-6))^2+(x(16)-b(i-6))^2);
f2= f2 + s(i)*x(i); %B(x15,x16)到各工地的吨公里数 end
f=f1+f2; % 总的目标函数

%主程序 
clear
x0=[3 50 7 0 1 0 0 4 0 6105127]'; 
A=[1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0]; 
B=[20;20];
Aeq=[1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0  
0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 
0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 
0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 
0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0];
Beq=[3;5;4;7;6;11]; 
LB=[zeros(12,1);-inf;-inf]; 
UB=[];
[x,fval,exitflag]=fmincon('liaoch',x0,A,B,Aeq,Beq,LB,UB)