阅读数模培训PPT的笔记
线性规划模型
例题1
任务分配问题:某车间有甲、乙两台机床,可用 于加工三种工件。假定这两台车床的可用台时数分别为800和 900,三种工件的数量分别为400、600和500,且已知用三种 不同车床加工单位数量不同工件所需的台时数和加工费用如 下表。问怎样分配车床的加工任务,才能既满足加工工件的 要求,又使加工费用最低?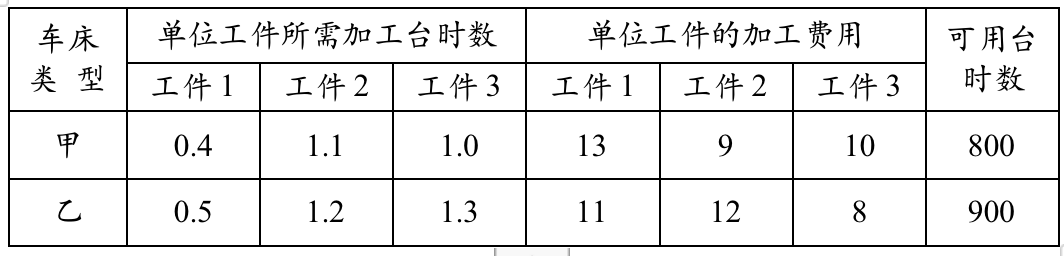
线性规划模型一般形式
目标函数+约束条件
$$
\min u= c^T x
$$
$$
\text { s.t.}
\left \lbrace \begin{array}{ll}&A x \leq b \\
& x \geq 0
\end{array}
\right.
$$
MATLAB实现
linprog 函数
linprog 是一个线性规划求解器,用于解决线性规划问题。它可以找到一组变量的最优解,使得目标函数达到最小值或最大值,同时满足一组线性约束条件。
模型:
$$
\min z=c^T x \\
s.t. \left \lbrace \begin{array}{ll} A_{ub} x \leq b_{ub} \\
A_{eq} x = b_{eq} \\
x \in bounds
\end{array} \right.
$$
使用方法:result = linprog(c, A_ub, b_ub, A_eq, b_eq, bounds)result = linprog(c, A_ub, b_ub, A_eq, b_eq, lb,ub[,x0])[result, fval, exitflag, output] = linprog(...)
参数说明:
- c: 目标函数的系数向量
- A_ub: 不等式约束条件的系数矩阵
- b_ub: 不等式约束条件的右侧常数向量
- A_eq: 等式约束条件的系数矩阵
- b_eq: 等式约束条件的右侧常数向量
- bounds: 变量的取值范围
- lb,ub: 变量的下界和上界(不和bounds同时使用)
- x0: 变量的初始值(可选)
- fval: 目标函数的最优值
- exitflag: 求解器的退出标志
- output: 包含有关求解过程的信息的结构体
返回值:
- result: 包含最优解和其他求解信息的对象
注意:当求解条件为最大值时,传入linprog时将目标函数的所有系数取反即可,即
$$
\max z=c^ T x \rightarrow \min z’=(-c)^T x
$$result = linprog(-c, A_ub, b_ub, A_eq, b_eq, bounds)
示例:
1 | % 目标函数系数 |
多目标线性规划模型
对于多目标线性规划模型,可以通过给定一个权重向量,将多个目标函数转化为一个目标函数,然后使用linprog函数求解。
例题2 1998年全国数学建模竞赛A题:投资的收益和风险
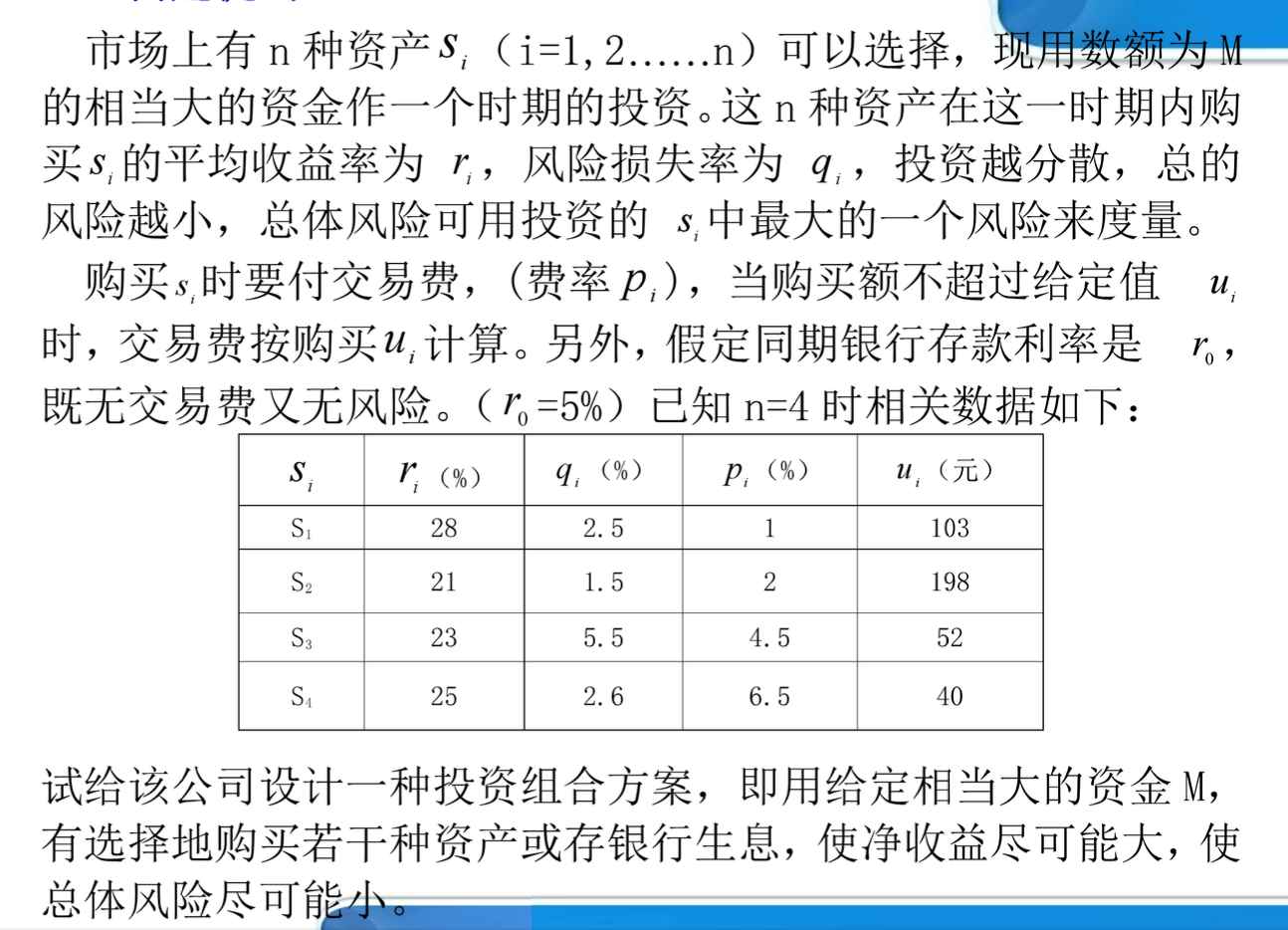
一、基本假设
投资数额M相当大,为了便于计算,假设M=1;
投资越分散,总风险越小,收益越稳定;
总体风险用投资项目$s_i$中最大的一个来度量;
n种资产$s_i$之间是相互独立的;
在投资的这一时期,$r_i,p_i,q_i,r_0$为常数。
净收益和总体风险只受$r_i,p_r,q_i$的影响,不受其他因素影响。
二、符号规定
- $s_i$表示第i种投资项目;
- $r_i,p_i,q_i$分别表示第i种投资项目的平均收益率,交易费率,风险损失率;
- $u_i$,$s_i$的交易定额
- $r_0$,同期银行利率
- $x_i$投资项目$s_i$的资金
- $a$投资风险度
三、模型分析




四、模型1的求解
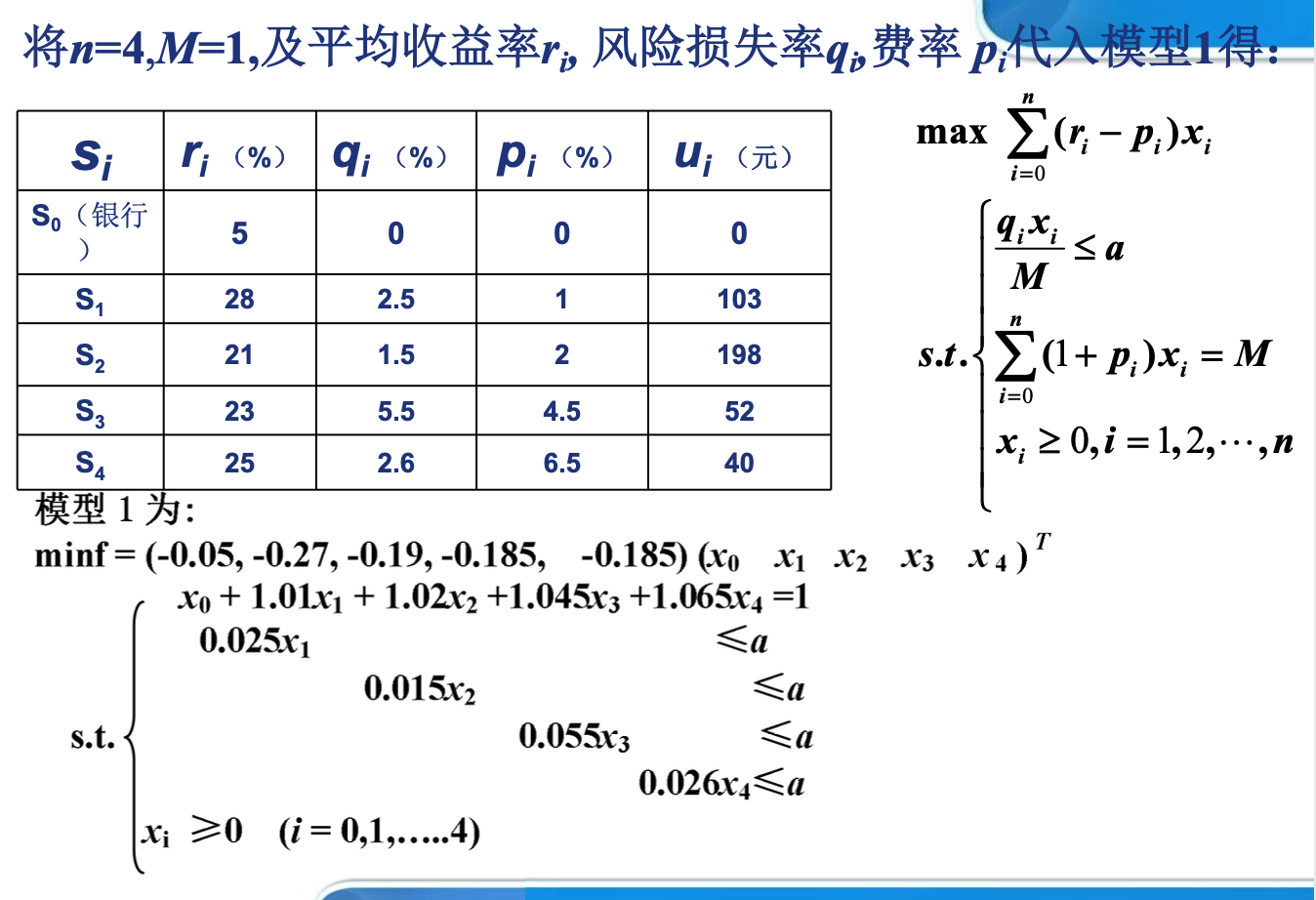


五、结果分析




