Mathematical Logic [Lec06 Proof Systems and Hilbert-style]

CS 210: Mathematical Logic Notes

Proof Systems

Types of Proof Systems

1. Hilbert-style system 希尔伯特风格系统（$\Sigma \vdash_{H}A$）：many axioms and only one rule.The deduction is linear.
2. Natural Deduction system自然演绎系统（$\Sigma \vdash_{ND}A$）：Few axioms(even none) and many rules The deductions are tree-like .
3. Resolution 归结系统（$\Sigma\vdash_{Res}A$）：used to prove contradictions

Hilbert-style Proof System

分离规则：如果有前提

1. A为真
2. A可以推出B
   那么可以推出结论：B为真

推理链

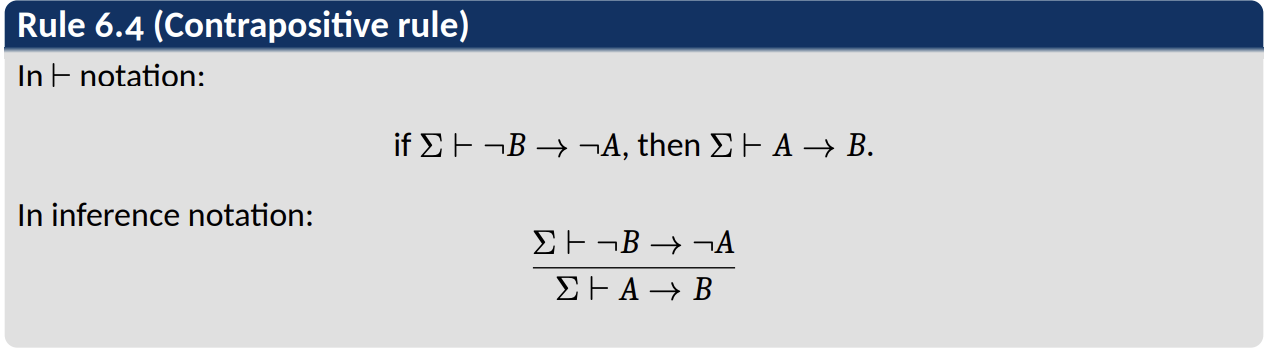
Derived rules in $\mathcal{H}$ 衍生规则

1. 反证法
   
2. 演绎法
   
   当且仅当在$\Gamma$成立的的系统下A可以推理出B时有“$\Gamma \cup {A}$“成立的系统下可以推理出B。
   使用演绎法可以推理出下面这个结论
3. Transitivity rule 传递率
   
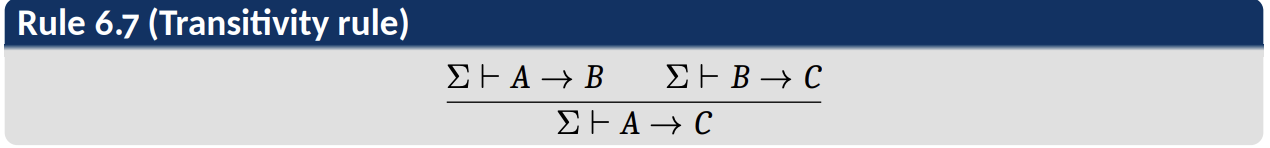
4. Exchange of antecedent rule 交换律
   
5. Double negation rule 二次取反规则
   
   
6. 反证法2
   

$$
\vdash (\lnot A \rightarrow A)\rightarrow A
$$